notes

In here are the list of things I did for a particular hour or day. Also included here are the screenshots of games I played, or videos I watched or listened to, or just random things I stumbled upon. I'll occasionally write down what I'm thinking, or things I'm planning to do.

[ 2024-02-26 ]

19:59 [link] [context] #sn

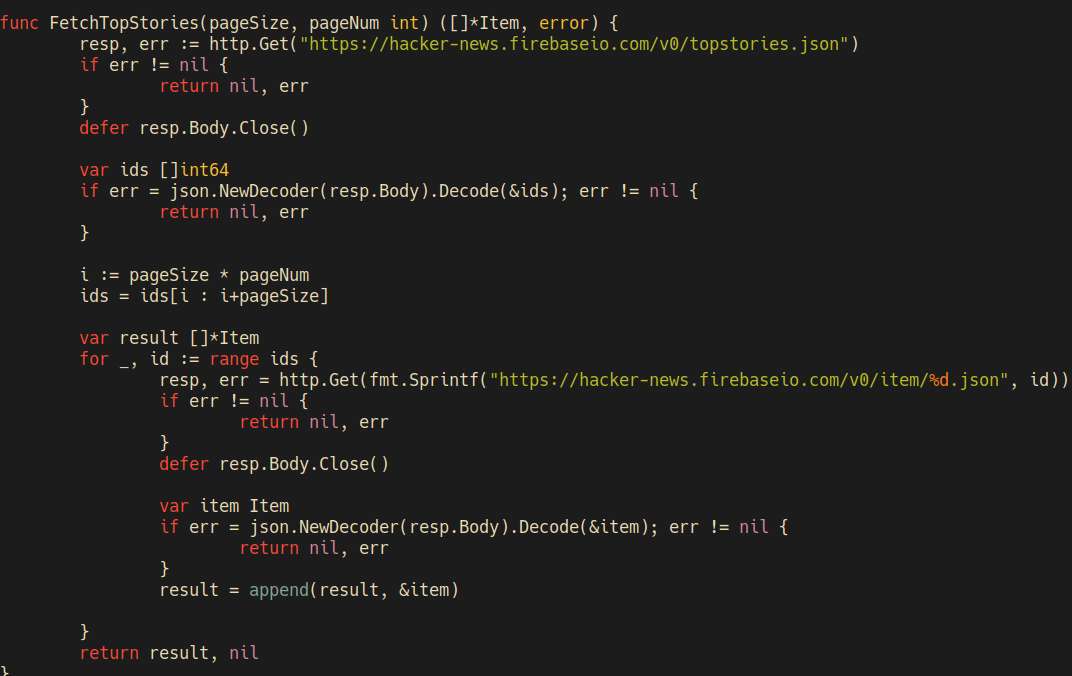
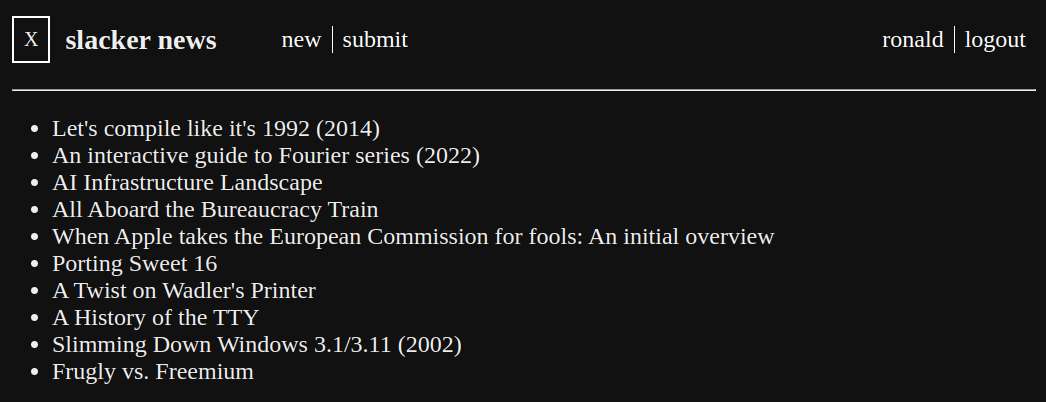
I decided to use the official HN api while creating the frontend first. That way, it's easier to create a compatible backend later on.

🕒 15:10

🕑 14:57

🕛 12:01

🕚 11:55

11:17 [link] [context] #math

Aha, I think I understand now. ∆y/∆x ≈ f'(x) does actually makes sense. I had an imprecise definition of derivative in my head. More precisely, the derivative f'(x) is

 f'(x) = st(∆y/∆x)

where the function st removes all the infinitesimal. ∆y/∆x is infinitely close to f'(x), which is to say their difference is infinitesimal, because:

   f'(x) - (∆y/∆x)
 = st(∆y/∆x) - ∆y/∆x
 = ε

With that, the proof of increment theorem would be:

 ∆y/∆x ≈ f'(x)
 ∆y/∆x - f'(x) = ε     // by definition of infinitesimal
 ∆y/∆x = f'(x) + ε      
 ∆y    = f'(x)∆x + ε∆x

I was previously wondering why ∆y would be an infinitesimal based on the increment theorem, but now it's clear that f'(x) is a real number, and based on the rules for infinitesimal arithmetic, f'(x)∆x + ε∆x would be indeed an infinitesimal.

I did consider and downloaded other books about infinitesimal calculus, but I didn't find any mention of the increment theorem. It would probably be better if I skim through at least one of them, to further solidify my understanding. In the end the wikipedia page was enough to clear up my understanding. Or maybe, a weekend break, consisting of turning my brain off.

I'll spend more time getting used to the notation shown on page 56, and I'll need to have a very intuitive understanding of increment theorem, because it seems important to gloss over.

🕚 11:03

🕙 10:24

🕙 10:23

🕔 05:13

🕔 05:03

🕔 05:00

🕒 03:20